突破!数学家又解决了一个数学难题!
拉姆齐数是一个看似简单却又难以捉摸的数学概念,它描述了一个群体中需要有多少个元素才能保证其中一定数量的元素之间存在某种联系。
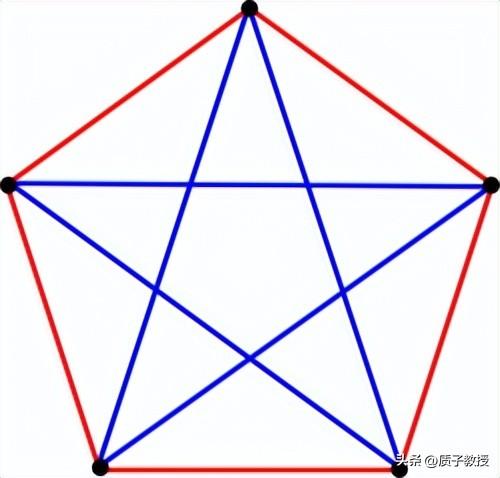
在组合数学上,拉姆齐定理,又称拉姆齐二染色定理,断言对任意正整数k和l,若一个聚会的人数n足够大,则无论相识关系如何,必定有k个人相识或l个人互不相识。
一个常用的比喻是聚会:你需要邀请多少人参加一个聚会,才能保证一定会有三个人彼此认识,或者三个人彼此陌生?对于3来说,拉姆齐数是6。如果你想保证一定会有四个人彼此认识,或者四个人彼此陌生,你就需要把宾客名单扩大到18。但是对于5来说,拉姆齐数是多少呢?
克莱布什图
数学家只能说它在43和48之间。而随着数字变大,这个问题就变得越来越难以解决。网络中的节点越多,可能的连接和结构就越多。“有太多的可能性,以至于你无法用暴力方法来解决它”,巴西纯粹与应用数学研究所(IMPA)博士生马塞洛·坎波斯(Marcelo Campos)说。他是这项研究的合著者之一。

埃尔德什·帕尔,其音读作air-dish,匈牙利语中的意思是来自山林,英语中作保罗·埃尔德什。匈牙利籍犹太人,发表论文高达1525篇,为现时发表论文数最多的数学家;曾和511人合写论文。
数学家可以给出任意一个拉姆齐数的范围。1935年,数学家保罗·埃尔德什(Paul Erd?s)发现了任意一个拉姆齐数的最大值是4的N次方。1947年,他又发现了任意一个拉姆齐数的最小值是2的N次方开平方。然而,在这两个上下界之间,还有很大的空间,而研究人员已经试图缩小这个差距几十年了。“基本上,这个界限一直卡在那里”,加州理工学院(Caltech)数学教授戴维·康伦(David Conlon)说。
但现在,坎波斯和他的同事们在这个上界上取得了进展:他们可以说任意一个网络的拉姆齐数的最大值是3.993的N次方,而不是4的N次方。
他们是如何做到的呢?他们利用了一种叫做“正则性引理”的工具,它可以将复杂的网络分解为更简单、更规则、更容易处理的子网络。“正则性引理”本身并不新鲜,它已经存在了几十年,但它非常难以应用。“它非常强大,但也非常抽象”,坎波斯说。“你必须找到一种方法来使用它。”
坎波斯和他的同事们找到了一种方法。他们首先将网络分成两部分:一部分包含所有节点之间可能存在的连接,另一部分包含所有节点之间实际存在的连接。然后,他们用“正则性引理”来分析第一部分,找出其中的规律和结构。接下来,他们用一种叫做“容器方法”的技术来处理第二部分,找出其中的异常和变化。最后,他们将两部分结合起来,得到了一个更精确的上界。
这个方法的优点是它可以适用于任何网络,而不仅仅是拉姆齐数问题。“我们的结果是非常一般的,它可以应用于任何类型的图论问题”,坎波斯说。“我们希望这个方法能够激发更多的研究和进展。”
康伦说,这项研究是一个“非常漂亮”的结果,它展示了数学家如何利用不同的工具来解决难题。“这是一个非常困难的领域,所以任何进步都是非常令人兴奋的”,他说。
拉姆齐数问题虽然看起来很抽象,但它实际上与现实生活中的许多问题有关。例如,它可以帮助理解社交网络中的群体形成,或者加密系统中的安全性。“拉姆齐数问题是一个很基本的问题,它涉及到很多其他领域”,坎波斯说。“如果我们能够更好地理解它,我们就能够更好地理解其他问题。”
[1] Stephanie Pappas. Mathematicians make rare breakthrough on notoriously tricky ‘Ramsey number’ problem. Live Science, 28 March 2023. https://www.livescience.com/mathematicians-make-rare-breakthrough-on-notoriously-tricky-ramsey-number-problem[2] Hannah Fulk. Mathematician uncovers methods to shrink sampling errors in large-dimensional data sets. Phys.org, 9 hours ago. https://phys.org/news/2021-03-mathematician-uncovers-methods-shrink-sampling.html[3] Flipboard. Mathematicians make rare breakthrough on notoriously tricky ‘Ramsey number’ problem. Flipboard, 2 hours ago. https://flipboard.com/topic/floridastateuniversity/mathematician-uncovers-methods-to-shrink-sampling-errors-in-large-dimensional-da/a-Og50NqKBQm-hpF6rTKcW-g%3Aa%3A2530880263-461cdc01b7%2Fphys.org
量子力学五大预言:五大量子力学的发现(量子力学的意义)
量子力学中的五大预言分别为波函数假设量子态演化,假设算符,假设测量假设以及量子全同性假设。量子力学是整个物理学中非常重要的一个学科,随着时代在不断发展,量子力学同样也发挥着至关重要的作用。世界上有无数的物理学家想要揭开威力的秘密,就必须要潜心研究量子力学。一、波函数假设我要新鲜事2023-05-13 09:05:070002中国四大名锦是什么?(云锦、蜀锦、宋锦、壮锦)
锦是一种丝织品,通常是指具有多种色彩和花纹的丝织物,要求极高,制作难度大,因此也十分名贵,被看作是丝织品中的最高技术工艺的代表,我国有四大名锦,分别是南京云锦、广西壮锦、苏州宋锦、成都蜀锦,那么接下来我们就一起去了解一下四大名锦吧!南京云锦我要新鲜事2023-05-13 12:08:550000只剩23台 用完火箭发动机咋办 骑扫帚飞!(RD-180发动机)
俄罗斯航天局停止供应火箭发动机后,美国仅剩的23台根本不够使用,俄方表示让他们骑着扫帚去飞。美国“星际航线”的成功发射,或许未来能够把宇航员送上国际空间站,尽管看起来前景光明,可是运载火箭的发射次数是有限的。宇宙神5号运载火箭我要新鲜事2023-04-02 01:42:470000皇太极怎么死的?根据史料推测有可能是热血病
皇太极是清朝的开国皇帝,他的战功非常的显赫。是我国历史上有名的政治家、战略家和军事家。但是,皇太极的去世却让许多学家们产生一些疑惑,毕竟史书上也没有详细的记录。所以,现在许多学家都在研究皇太极怎么死的。一、皇太极是生老病死的我要新鲜事2023-05-11 09:52:040000亚马逊原始森林有多可怕?恐怖生物让人危险重重
导语:亚马逊原始森林位于南美洲的亚马逊平原,占据了全球森林面积的20%,但这里让人恐怖的不是高温潮湿的环境,而是神秘的原始部落,过于庞大的森林面积,湍急的地下暗河,奇异的神秘物种和剧毒的危险生物,下面探秘志就带大家共同了解。1、神秘部落我要新鲜事2023-05-09 09:44:140000






