逻辑回归
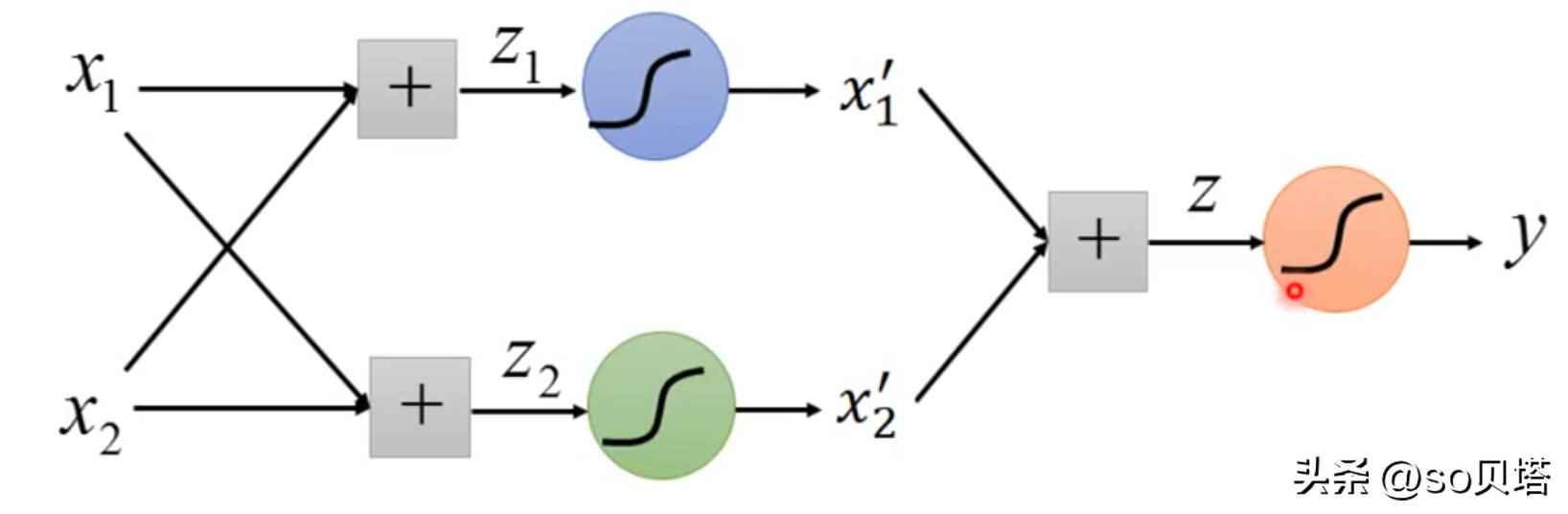
逻辑回归的原理是用逻辑函数把线性回归的结果(-∞,∞)映射到(0,1)
线性回归函数
线性回归函数的数学表达式:
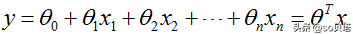
其中xi是自变量,y是因变量,y的值域为(-∞,∞),θ0是常数项,θi(i=1,2,...,n)是待求系数,不同的权重θi反映了自变量对因变量不同的贡献程度。
我们初中学过的一元一次方程:y=a bx,这种只包括一个自变量和一个因变量的回归分析称为一元线性回归分析。
初中学过的二元一次方程:y = a b1x1 b2x2,三元一次方程:y = a b1x1 b2x2 b3x3,这种回归分析中包括两个或两个以上自变量的回归分析,称为多元线性回归分析。
不管是一元线性回归分析还是多元线性回归分析,都是线性回归分析。
逻辑函数(Sigmoid函数)
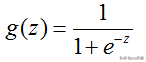

极大似然函数
先来看一个小例子:如果小华这次考试考了90分以上,妈妈99%会奖励小华一个手机,如果没有考到90分以上,妈妈99%不会奖励小华手机。现在小华没有得到手机,问小华这次有没有考到90分。
可能我们的第一反应是小华大概率没有考到90分以上。这种利用已知样本结果,反推最有可能导致这样结果的参数值,就是极大似然估计。
结合逻辑回归函数,如果我们已经积累了大量的违约客户和正常客户的样本数据,利用极大似然函数由果溯因,估计出使得目前结果的可能性最大参数(系数)θ,有了参数我们就可以求任何一个客户违约的概率了。
我们上文提到过客户违约的后验概率

相应的可以得到客户不违约的概率:

如果令

违约的后验概率可以写成:
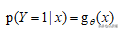
不违约的后验概率可以写成:

对于某一个客户,我们采集到了样本数据(x,y)。对于这个样本,他的标签是y的概率可以定义成:

其中y∈{0,1}。当y=0时,上式为不违约的后验概率,当y=1时,上式为违约的后验概率。
现在我们有m个客户的观测样本

将每一个样本发生的概率相乘,就是这个合成在一起得到的合事件发生的总概率(利用概率中的乘法公式),即为似然函数,可以写成:

其中θ为待求参数。
注:我们总是希望出现目前结果的可能性最大,所以想要得到极大化似然函数对应的参数θ。
为便于求解,我们引入不改变函数单调性的对数函数ln,把连乘变成加法,得到对数似然函数:

至此,可以用梯度上升法求解对数似然函数,求出使得目前结果的可能性最大的参数θ。也可以由对数似然函数构造损失函数,用梯度下降法求出使得损失最小对应的参数θ,接下来看下逻辑回归中的损失函数。
注:使用对数似然函数,不仅仅把连乘变成加法,便于求解,而且对数似然函对应的损失函数是关于未知参数的高阶连续可导的凸函数,便于求其全局最优解。
构造损失函数
在机器学习中有损失函数的概念,我们知道损失函数一般定义为预测值和真实值的差,比如我们预测小华在这次考试中能考98分,成绩出来了小华实际考了97分,小华的成绩预测值和真实值差为1,这个1通俗理解就是损失函数的值。
从上面的案例知,如果损失函数越小,说明模型预测越准。所以在函数比较复杂没有确定解(解析解)或很难求出确定解的情况下,一般求的是数值解(近似解)。一般模型求数值解可以求出使得损失函数最小对应的参数θ。
结合逻辑回归中的极大似然函数,如果取整个数据集上的平均对数似然损失,我们可以得到:

其中J(θ)为损失函数,由对数似然函数前面添加负号取平均得到。
即在逻辑回归模型中,最大化似然函数和最小化损失函数实际上是等价的(求最大化对数似然函数对应的参数θ和求最小化平均对数似然损失对应的参数θ是一致的),即:

那如何求得损失函数最小对应的参数呢?可以用下节讲到的方法:梯度下降法。
用梯度下降法求解参数
先以一个人下山为例讲解梯度下降法的步骤:
step1:明确自己现在所处的位置;step2:找到现在所处位置下降最快的方向;step3: 沿着第二步找到的方向走一个步长,到达新的位置,且新位置低于刚才的位置;step4:判断是否下山,如果还没有到最低点继续步骤一,如果已经到最低点,则停止。
从上面的分析知,用梯度下降法求解参数最重要的是找到下降最快的方向和确定要走的步长。
那么什么是函数下降最快的方向?
如果学过一元函数的导数,应该知道导数的几何意义是某点切线的斜率。除此之外导数还可以表示函数在该点的变化率,导数越大,表示函数在该点的变化越大。

可以发现p2点的斜率大于p1点的斜率,即p2点的导数大于p1点的导数。
对于多维向量
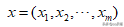
它的导数叫做梯度(偏导数),当求某个变量的导数时,把其它变量视为常量,对整个函数求导,也就是分别对于它的每个分量求导数,即

对于函数的某个特定点,它的梯度就表示从该点出发,函数值变化最为迅猛的方向。至此梯度下降法求解参数的方向已经找到,那就是函数的梯度方向。
接下来推导损失函数的梯度(偏导数):
由损失函数的公式知:

对损失函数求偏导:
损失函数 J(θ)中,是 θ和 x 都是一个向量形式,也就是:
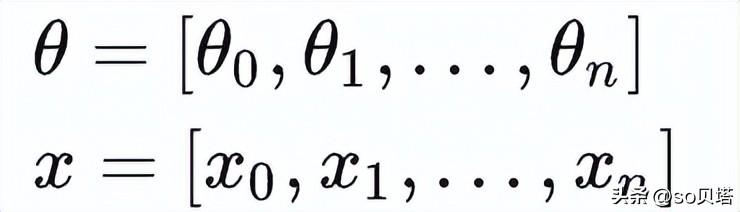
当我们仅仅针对θ进行求导的时候:

可以看到上面需要利用sigmoid函数的求导方法:

至此,LR的损失函数的求导形式已经结束,这里面主要用到了sigmoid函数的求导,推导起来其实是比较简单的。最后写出梯度下降的更新公式:

韦伯发现化石星系,内部已不再产生恒星,或将改写宇宙年龄
在我们的宇宙中,大约有2万亿个星系存在,银河系只是其中之一,而且还是一个比较年轻的星系,因为它内部仍有恒星诞生。然而在有些星系里,氢元素的密度已经不足以再形成新的恒星了,所以这种星系只能是宇宙大爆炸之初就存在的星系,也被称为宇宙化石星系,通过研究它们,天文学家就能复原宇宙大爆炸早期的宇宙状态。韦伯望远镜目前就发现了这种星系我要新鲜事2023-10-01 18:19:350000石楠花为什么这么臭?石楠花为什么闻起来像精液(胺类物质)
解答:石楠花是一种让人感觉复杂的花朵,主要是因为奇妙的气味。专业的植物专家表示,石楠是蔷薇科苹果亚科石楠属,这一亚科的山楂属、栒子属等等都有奇怪的气味,实际上是因为挥发成分中的胺类物质在作怪,石楠花的奇妙气味可能也和胺类物质脱离不了关系。石楠是什么?石楠本来名字是石南,早在很早之前汉末成书的《名医别录》中就有所记载了,按照李时珍的说法,这种植物喜欢生长在石头间向阳的地方,所以被称为石南。我要新鲜事2023-05-10 05:49:250000宇宙究竟有多大?望远镜拍摄的照片让人绝望(没有解释)
宇宙是人类一直不断进行着探索的地方,可是直到现在人们也不知道宇宙底有多大,宇宙究竟有没有边界,这些都是未知数。不过根据科学家研究发现,宇宙是在一直膨胀的,但是以目前人类的科技和水平无法跟上宇宙膨胀的速度。根据美国人在韦伯望远镜上拍摄的照片,可以发现宇宙的深处是一片漆黑,所以说可以解释为目前宇宙没有尽头,就算引有尽头,也是人类探索不到的地方。这张望远镜拍摄的照片如此之大,不过也仅仅只是一个星系。我要新鲜事2023-05-14 15:21:400000围绕着地球的人造卫星 对人类有什么作用(人造卫星)
GPS和数据传输需要依赖人造卫星。人造卫星在当今时代,人造卫星已经成为了我们生活中不可或缺的一部分。它们在许多方面都为人类提供了巨大的帮助,从天气预报到全球定位系统,再到电视和广播信号传输,人造卫星的影响无处不在。人造卫星在气象监测和预报方面发挥着至关重要的作用。通过搭载各种气象仪器,人造卫星能够全天候监测地球的气候变化,提供关于温度、湿度、气压、风速等信息。卫星作用我要新鲜事2024-01-11 19:38:460000宇宙大脑极其相似 是否可以解释宇宙(宇宙奥秘)
宇宙可能是某个生物的大脑结构。自从人类发现宇宙之后,就不止一次的想过宇宙的真实情况是怎么样的?对于人类现在来看,宇宙绝对是一个让人类无法超越的区域,毕竟我们人类如今已经有了比较发达的科技水平,可是凭借着这样的科技水平也只能够在地球的周围稍微活动一下,根本无法突破地球周围的限制没有办法去突破太阳系,更不要说是去探索整个宇宙了,但是科学家们在对于宇宙研究这些年以来也有了一些惊人的发现。1.惊人发现我要新鲜事2023-09-20 20:26:130000






