平行线居然能相交 这是不是已经和常识矛盾(黎曼几何)
我要新鲜事2023-05-15 18:08:150阅
黎曼几何验证平行线也有相交的可能。为什么平行线在非欧几里得几何中相交?长期以来,我们一直被告知,在同一平面上永不相交的两条直线被称为平行线,但事实上,这只是欧几里得几何的一个理论,主要适用于我们的日常生活。除此之外,还有非欧几里得层次。与欧几里得几何不同,几何体系主要包括罗氏几何和黎曼几何。
第五公设
开头提到的数学学科是罗氏几何的鼻祖。罗巴切夫斯基一直想证明欧几里得几何中的第五个公设,即公社相当于越过一条线,特别是在只有一条线与这条线平行的情况下。在无法证明的情况下,罗巴切夫斯基开始使用反证法,即只要能证明线外的一点能使至少两条线平行于已知的线,那么就能证明第五公设不义。

无限延伸的线
最终,罗巴切夫斯基在马鞍脸上找到了答案。事实上,几何上最大的不同在于它是以空间为基础的。在一个非零气质的飞机上。在所谓的非欧几里得几何中,要理解平行线的交点,可以从球面进行简单的理解。如果我们在球面上取任意两点,我们会发现球面上两点之间的最短距离就是大圆的坏部分。大圆是球面上两点之间的短大圆弧。我们之前学过两点之间最短的线段,线段在两端无限延伸形成一条直线,所以只有球面上的大圆是直线。

黎曼几何的假设
例如,经线和纬线。所有的都是直线,除了赤道在违章建筑中不是直线。既然赤道大圆是一条直线,那么发现源也是一条直线,所有的发现源都垂直于赤道大圆,那么所有的经线应该是平行的。但是我们知道它们都在南北两极相交,所以平行线在一定距离上相交,或者说球面上所有的线都相交,这就是黎曼几何的假设。
0000
评论列表
共(0)条相关推荐
日本曾经制作出来的气球炸弹,到底是怎么一回事?(气球炸弹)
日本的气球炸弹一点儿作用都没有大家每次在看到气球的时候都会认为这是一种玩具,不管是以前还是现在都是,但是大家有没有想过利用气球也是可以杀人的?日本人曾经就有过这么一个想法,还是在二战时期,那么利用气球该怎么杀人呢?日本人又为什么要这样做?我们就来看一看这是怎么回事吧。日本人的气球炸弹我要新鲜事2023-05-15 11:37:060000到底是什么赋予了万物的质量(希格斯粒子)
我们身处宇宙之中,被无数的物体和现象所包围,而这些物体都具有质量。但是,我们或许很少思考过,到底是什么赋予了这些物体质量?这个问题的答案涉及了物理学的深奥领域,其中一个关键角色就是希格斯粒子。质量的定义在物理学中早已有之,它以牛顿第二定律和万有引力定律为基础,分别涉及到惯性质量和引力质量。然而,这些定义并没有揭示质量的本质。我要新鲜事2024-02-16 20:28:210000阿莱悖论通俗解释 阿莱悖论和股票的关系
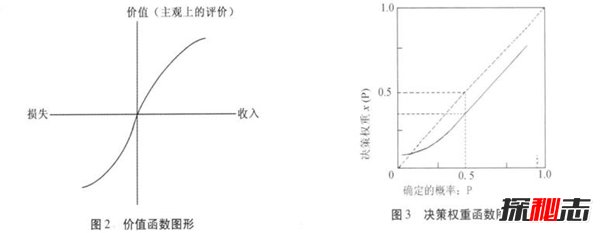
导语:阿莱悖论是由法国的经济学家在1952年提出的,为了更好的证明预期效用理论,也就是大家会在比较确定的好处,也就是收益和赌一把中做出相应的选择,但是更多的人会选择比较确定的好处,人们总是在盈利的时候害怕风险,而在亏损的时候又热爱风险,下面探秘志带大家认识一下阿莱悖论。阿莱悖论具体内容来自法国的著名经济学家、诺贝尔经济学奖获得者阿莱做出了一个比较有名的实验。对100人测试所设计的赌局:我要新鲜事2023-05-09 00:57:020000蚂蚁意识不到人类的存在,就像人类意识不到高级外星文明的存在?
首先来讲,蚂蚁能够意识到人类的存在,但它们并不知道人类是智慧物种,在蚂蚁眼里,人类与其他物种并没有什么不同。蚂蚁的眼神确实不太好,看任何东西基本都是一片模糊,如果距离不是太远,能看到人在活动,但并不知道人类是个什么东西。蚂蚁生活的世界一片模糊,它们看到的东西就像我们看到的打了马赛克的世界一样。不仅模糊,而且没有颜色。我要新鲜事2023-05-13 19:00:100000机器人也拥有了身份 并且扬言摧毁人类(机器人类)
拥有身份的机器人所说出的话应该是有人后台控制。现在我们可以从科幻电影当中看到一些人工智能的样子,人工智能也可以从某些方面上帮助人类做很多事情,在早些的时候,通过一些科幻电影就已经可以让人类意识到当下的问题有多么严重,如果人类在去肆意的对于人工智能进行发展,那未来很有可能人类的社会将会被人工智能给毁灭,在前些年的时候就已经出现了拥有身份的机器人。并且这个机器人还曾扬言说要毁灭这个世界。人工智能我要新鲜事2023-12-21 21:42:080002