数学里的自然常数e,被大神欧拉完美解决(欧拉数)
在数学领域,有许多有趣的常数,这些常数的起源一般都经历了波澜壮阔的数学进化史。比如我们之前提到的圆周率,这是比较常见的,小学阶段也能遇到。

今天我们要学的是自然常数e,这很重要。和π一样,它是一个无限的、非循环的小数。我们至少要在高中接触对数函数后才会接触到这个数,而要想完全了解这个数,至少要在大学学习高等数学。自然常数E经常出现在数学物理计算中,那么这样一个重要而特殊的数是怎么来的,又有哪些具体的实际意义呢?
在十八世纪初,有一位伟大的数学神,名叫欧拉。这个大家应该都很熟悉。他绝对是人类历史上最强大的五位数学家之一。自然常数E是这位数学家在求解复利问题时提出来的,因此E也被称为欧拉数。当n接近无穷大时,(1 1/n)n不是接近无穷大,而是等于2.71828这样的常数,这是一个无限的、非循环的小数,它像圆周率一样是无理的。后来为了便于记录,用字母E表示。
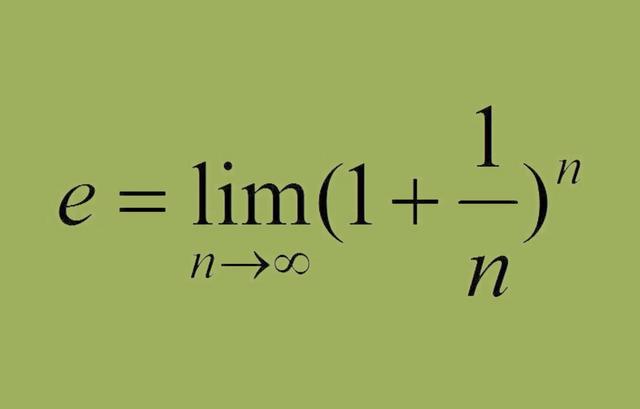
这个E是现在大家都习惯和常用的自然常量。E不是随机数。随着你对数学的学习越来越深入,你会逐渐发现它是数学中最有用的数字之一。当我们用镜像法画出y=ex的函数时,会发现对于这个函数曲线上的任意一点,它的斜率也是ex,也就是说y=ex的导数就是它自己。
不仅如此,这个函数的图围绕X轴的面积也是E X,而在函数y=n X中,只有当n=E时,这个方程才有这样神奇的性质。从这些例子中我们不难看出,自然常数e无疑是微积分领域中一个重要而特殊的数。
不仅如此,在物理学领域,自然常数E的应用也很广泛,通常以正态分布或与波有关的公式出现,如电磁波、声波、量子波等。除了上面的例子外,关于自然常数e还有一个非常著名的方程,即欧拉方程,也叫欧拉恒等式:e(iπ) 1=0。这个公式可以说是数学发展至今出现的最漂亮的公式。这个公式同时完美地连接了数学中最重要的数。
双角犀鸟是什么种类的鸟?只分布在我国的云南地区!
双角犀鸟是一种体长1.2米的大型鸟类,翅膀可达1.6米。在它们巨大的体型之下,它们还有一张大嘴,这是它们最特别的部分。二角犀鸟的嘴长约30厘米。嘴的上方有一个又宽又大的头盔突起,有点像犀牛的角。“犀牛”这个名字是因为头盔突起的存在。一般来说它们的头盔和上喙呈橙黄色,下喙呈灰白色。它们的腹部和尾羽是白色的,其余的羽毛是黑色的。体型大颜色鲜艳,在野外其实很容易辨认。我要新鲜事2023-05-17 05:48:550000赘婿中宁毅12个女人都有谁:没有十二个(苏檀儿为发妻)
之前网络上出现了许多根据小说改编而成的影视作品,比如说《庆余年》,一经播出,反响巨大,至今仍然有人打探《庆余年2》什么时候上映,而《赘婿》也被改编成了电视剧,其中男主有很多妻子,那么赘婿中宁毅12个女人都有谁呢?接下来我们就一起去了解一下吧!赘婿中宁毅12个女人都有谁我要新鲜事2023-05-14 21:42:160000红薯不能和什么一起吃 红薯为什么不能和这些一起吃
红薯是生活中常见的食物,它的营养价值比较高,味道也挺不错。不过红薯也不能和以下食物搭配,一起吃可能引起不适,这些食物分别是鸡蛋、鸡肉、螃蟹、酒和柿子等,假如一起吃会有不良反应。红薯不能和什么一起吃1.鸡蛋:不管是红薯还是鸡蛋都是比较难消化的,假如一起吃的话可能让消化不良症状更重一些,甚至会引起身体的不适导致腹痛等等,所以建议红薯不要和鸡蛋一起吃。我要新鲜事2023-05-11 02:14:020000妲己古尸容貌复原图,历史上妲己红颜祸水的狐媚之相
妲己因为《封神演义》中心狠手辣的狐狸精而为人熟知,妲己古尸容貌复原图也的确有红颜祸水的狐媚之相。妲己墓在河南淇县被发现,十分荒凉,妲己古尸印证了历史记载,能让年过六十的纣王每日沉迷美色之姿,最后的结局也很凄凉。一、妲己墓被发现我要新鲜事2023-03-15 01:42:410002巴西男子街头绑走12岁女童性侵 为何会产生恋童癖
在巴西鲁兹安尼亚,一名42有着恋童癖的男子,将一名12岁的女童迷晕后性侵。这名男子在街头独自将上学的女孩绑走后,装进了行李箱当中,一路拖拽着回到了公寓,当警方找到女孩时,发现女孩双脚已经被扣住并且昏迷了,这一名男子之外还有23岁的另外一名女子被逮捕,也被指控协助做案将这名女孩迷晕。我要新鲜事2023-07-05 19:11:130003






