数学家发现了爱因斯坦瓦片,它可以无限铺满一个平面而不会重复
数学家们发明了一种新的13边形,可以无限地铺满一个平面,而不会出现重复的图案。他们称之为“爱因斯坦瓦片”。这个词并不是来自著名的物理学家阿尔伯特·爱因斯坦,而是来自他姓氏的德语翻译:一块石头。

数学家们对这个问题感兴趣已经有几十年了。早在1961年,数学家王浩就提出了一个猜想,认为无周期平铺,即永远不会成为重复图案的平铺,是不可能的。但他自己的学生罗伯特·伯格尔却证明了他错了,他找到了一组20,426个形状,当仔细排列时,永远不会重复。
他后来将这个集合缩减到了104个瓦片。这意味着如果你买了一套这样的瓦片,你可以把它们排列在你的厨房地板上,永远不会找到一个重复的图案。

彭罗斯平铺包含多种对称性,但它永远无法周期性重复。
在20世纪70年代,诺贝尔奖获得者、物理学家罗杰·彭罗斯发现了一组只有两个瓦片的集合,它们可以以非重复的方式排列在一起,现在被称为彭罗斯平铺。
从那时起,世界各地的数学家们都在寻找无周期平铺的圣杯,“爱因斯坦瓦片”。他们是否能找到一种单一的形状能够填充一个二维空间,而不会重复它所创造的图案呢?
答案刚刚被英国东约克郡一位退休印刷技术员大卫·史密斯发现了。他是如何发现这个惊人的解决方案的呢?“我总是在摆弄和实验各种形状,”史密斯告诉《纽约时报》。
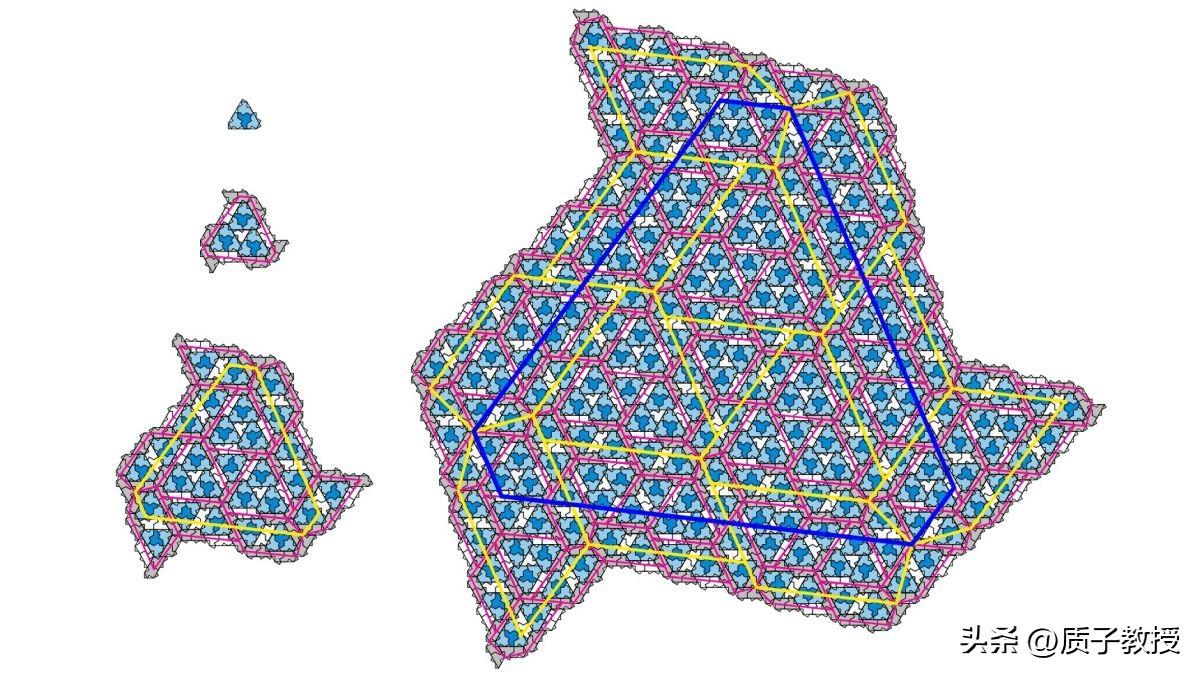
史密斯发现了一个13边形(也称为十三角形),它有一个特殊的性质:它可以被分成四个更小的相同形状(称为子瓦片),或者可以被组合成四个更大的相同形状(称为超级瓦片)。这意味着这个13边形可以无限地缩小或放大,并且可以用来铺满一个平面,而不会出现重复的图案。这就是“爱因斯坦瓦片”的定义。
史密斯的发现是数学界的一个重大突破,也是一个美丽的艺术作品。他的13边形有着复杂而优雅的对称性,可以创造出令人惊叹的图形。他还给他的形状起了一个有趣的名字:帽子(hat),因为它看起来像一个戴着帽子的人的轮廓。
史密斯并不是一个专业的数学家,但他对形状和图案有着浓厚的兴趣。他曾经设计过一种新型的拼图,叫做“史密斯拼图”,它由一些不规则的形状组成,可以拼成任何你想要的图案。他还曾经发明过一种新型的骰子,叫做“史密斯骰子”,它由一些不同形状的多面体组成,可以用来玩各种游戏。
史密斯说,他对“爱因斯坦瓦片”的灵感来自于一本关于无周期平铺的书籍,以及一些网上的资源。他用电脑软件来设计和测试他的形状,并与一些数学家和艺术家交流他的想法。他说,他花了大约两年的时间才找到了这个13边形,并证明了它是一个“爱因斯坦瓦片”。
史密斯说,他对自己的发现感到非常兴奋和自豪。“我觉得我做了一件很特别的事情,”他说,“我觉得我创造了一种新的美。”
史密斯和他的合作者们已经将他们的发现发表在了数学杂志《几何与拓扑》上,并得到了其他数学家们的认可和赞扬。他们还计划制作一些实体模型,以展示他们的形状在三维空间中是如何排列和变化的。
史密斯说,他希望他的发现能够激发更多人对数学和艺术之间的联系感兴趣,并且能够为未来可能有用的应用打开新的可能性。“我认为这是一个很有价值和有趣的领域,”他说,“我希望能够继续探索和创造更多。”
Sutter, P. (2023). Newly discovered ‘einstein’ tile is a 13-sided shape that solves a decades-old math problem. Live Science. Retrieved from https://www.livescience.com/newly-discovered-einstein-tile-is-a-13-sided-shape-that-solves-a-decades-old-math-problemSmith, D., Mannan, M., & Sadun, L. (2023). The first known example of an einstein. Geometry & Topology, 27(1), 1-25. doi:10.2140/gt.2023.27.1Penrose, R. (1974). The role of aesthetics in pure and applied mathematical research. Bulletin of the Institute of Mathematics and its Applications, 10(7/8), 266-271.Berger, R. (1966). The undecidability of the domino problem. Memoirs of the American Mathematical Society, 66, 1-72.Wang, H. (1961). Proving theorems by pattern recognition II. Bell System Technical Journal, 40(1), 1-42.
建筑上常见的避雷针 工作原理是什么(分散电流)
避雷针的工作原理是引导和分散顶流。避雷针作为一种常见的防雷装置,在我们的生活中有着广泛的应用。避雷针的诞生,源于人们对雷电灾害的认知。雷电是一种自然现象,当天空中的云层积累到一定程度后,会产生电荷,形成雷电。雷电的电流非常大,电压非常高,能够对地面上的建筑物和人类造成巨大的威胁。为了防止雷电灾害,人们发明了避雷针。工作原理我要新鲜事2024-01-23 21:09:380000哪些人群不适宜吃海参呢 海参的营养价值有哪些
小孩子不适合吃海参,有肝病的人群也不适合吃海参。海参是海鲜的一种,在营养物质中是大补,但是有些人适合吃,而有些人不适合吃。所以想要吃海参之前一定要咨询医生或者是咨询营养专家,这样是对自己的身体健康负责任,在饮食上一定要特别注意。一、具体解析不易吃海参的人群我要新鲜事2023-05-12 03:05:320000俄罗斯发射的超快飞行物,美国方面认为是太空设备(航天武器)
俄罗斯在航天设备方面有了最新的突破当大家提到关于外星人的科技和星球大战的时候,肯定都会想到各种各样花里胡哨的武器。就比如说最常见的激光剑就是如此。根据科学家所说,人类在未来也能够变成这样,只不过要真的像是科学家所说的这样。那人类可能还需要很长的时间。但是想要制造出一艘速度比较快的飞船,人类还是有办法的,比如说前一段时间俄罗斯就制造出来了一个.速度超快的飞船我要新鲜事2023-05-15 13:31:200000职业目标怎么写 怎么样对自己的职业进行合理的规划
职业目标顾名思义就是对于自己的职业规划,这也算是比较重要的东西,那么职业目标应该怎么写呢,小编带大家一起了解探索下。职业目标怎么写我要新鲜事2023-05-13 11:07:520000假如一个外星文明进攻地球 人类有没有反击的能力
如果外星人真的进攻地球,人类是否有能力战胜他们,苏联天文学家尼古拉·卡尔达舍夫曾提出了一个有趣的设想,即将外星文明划分为三个等级。一级文明:这种文明可以主宰它们所在的星球以及周围卫星的所有能源。二级文明:这种文明可以利用整个恒星系统的能源。三级文明:这种文明可以利用银河系中所有的能源。我要新鲜事2023-06-07 21:00:040000