贝特朗悖论,你所不知道的几何谜题(看完怀疑人生)
我要新鲜事2023-03-13 03:12:172阅
你听说过贝特朗悖论吗?
这是一个在几何概率领域的一个悖论,它的矛头直接对准了几何概率本身。
贝特朗悖论
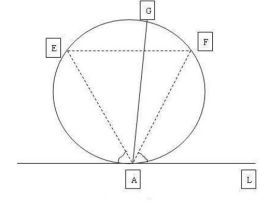
这个悖论的内容是:在一个圆内任意选一条弦,这条弦的弦长长于这个圆的内接等边三角形的边长的概率是多少?
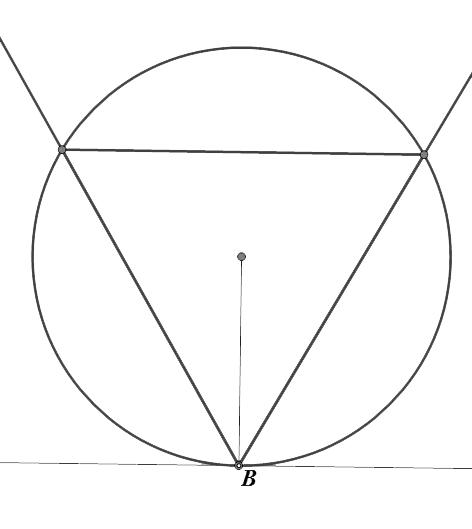
这看上去其实是一个并不难的概率问题,只需要根据圆本身的一些特性来计算就可以了。
但是问题在于,贝特朗给出了三个解法,每一个解法都十分正确,找不出任何问题。
但是,三个解法的答案却是不一样的。
关于这三种解法,我们在此不作叙述,感兴趣的可以去查找资料看一看。
这个悖论的问题在于,为何三个正确的解题思路,得出的答案却是不同的?

悖论为何会产生
这个悖论的出现,矛头直指几何概率,它的存在,似乎证明了几何概率完全是一个错误的存在。
这可不是一件小事,这意味着当时的整个几何概率体系都是建立在错误之上的。
可以说,这个悖论的出现,几乎推翻了古典几何概率体系。
而这个悖论之所以会产生,是因为三种解决问题的办法,用了不同的途径,有的用了边长,有的用了面积。
但是在古典概率体系中,把所有未知的概率都认为是等概率的。
比如,圆形的边长分布和面积分布都是未知的,因此它们都是等概率的。
但是这个悖论得出三个不同的答案,意味着其中至少有一个分布,并不是等概率。
几何与概率
几何学和概率学,都是数学里的重要组成部分。
我们从小学就开始学习圆形、长方形等简单几何,从初中就开始学习简单的概率题。
但是,尽管已经学习了很多,我们对于未知事物的概率问题仍然是会采用自己的第一印象的,这就会造成很多悖论的发生。
贝特朗悖论衍生出了很多概率悖论,比如贝特朗箱子悖论,都是因为人的第一反应而产生的错误。
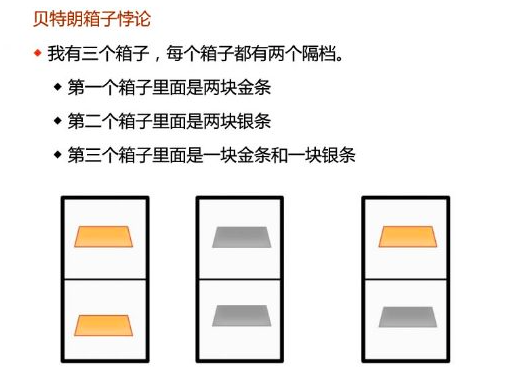
如果你觉得有趣,可以去找来测试一下自己会不会犯同样的错误。
0002
评论列表
共(0)条相关推荐
解析风流草的舞蹈,会跟随阳光而跳舞的植物(舞姿销魂)
你可能见过很多种奇形怪状的植物,但你绝对没见过一种会跟随阳光跳舞的植物。这种会跳舞的植物被人们称为风流草,风流草的舞蹈非常销魂,被人们称为是艺术家的舞蹈。这种风流草在中国部分地区也有生长,跟小编一起来看看风流草的舞蹈吧。跟随阳光而跳舞我要新鲜事2017-12-05 12:34:54000120分钟一起强奸案 居然连蜥蜴都不放(强奸大国)
印度是出现强奸案件最多的国家。那去年的四月就出现了一个超过了人们认知之外的事情,就是印度有四个男人和一个蜥蜴发生了性关系,并且其中还有一个人把全部的视频都给拍了下来。这样一个在全世界都会感觉到荒诞和理解的事情,居然在印度并没没有得到太大的反响,甚至有不少人觉得是正常的。而印度则是有着非常多的强奸案例。印度强奸案例我要新鲜事2023-05-12 04:05:470002因大臀部上畸形秀的南非女性 死后仍展出100多年 总算入土为安
她是莎拉·巴托曼。或许你曾在社交媒体或杂志封面上看到过一张照片,上面是卡戴珊用她丰满的臀部接住香槟的画面。这一令人印象深刻的瞬间,将一个酒杯平稳地摆放在她的臀部上,然后香槟顺着她的身体优雅地流入酒杯中。我要新鲜事2023-10-10 21:16:130000外卖小哥在路上撒图钉 最后被判刑(报复行为)
外卖小哥因为和他人发生口角,在路上撒下3000枚图钉。在前几天福建厦门的一个外卖小哥。因为和另外一个平台的外卖骑手因为一些小摩擦从而发生了口角,一怒之下就选择了用一些比较极端的方式来报复对方,在路上撒下了3000多枚图钉。报复行为我要新鲜事2023-04-03 01:01:420000全世界最胖的女模特 当她脱下外套瞬间 全场男士都沸腾了
泰斯·霍丽迪是全球最知名的大尺码模特之一,她的身材特点成为她在模特圈里的独特标志。泰斯·霍丽迪是一个非常特别的女人,她的身材特点和表现使她成为模特圈的独特风景。她的美丽和魅力不仅让人们看到身体,更让人们看到她内心的自信和勇气。她的故事鼓舞人心,鼓励人们勇敢坚持自我,展现真实的美丽和魅力。我要新鲜事2023-05-29 20:56:120009






